Square Root of 2 in Babylonian Mathematics and the Sulbasutras

On some claims by Neugebauer regarding the the square root of two in Babylonian mathematics and the Sulbasutras

Note: My book The Imperishable Seed: How Hindu Mathematics Changed the World and Why This History Was Erased, is available at
https://garudabooks.com/the-imperishable-seed
and
https://www.amazon.in/IMPERISHABLE-SEED-Mathematics-Changed-History/dp/B0BG7RRLVR

In a previous article I had discussed about the biases that exist in mainstream academic circles when it comes to the Sulbasutras and the many concessions made in favor of Babylonian mathematics, with the result that the latter dominates the discourse of the history of mathematics in ancient times, while the Sulbasutras barely get a passing mention. In addition, I showed how this attitude of sidelining the Sulbasutras is not a new phenomenon, but something that has been prevalent right since the time of Moritz Cantor soon after the Western world was introduced to them in 1875 through the writings of Georg Thibaut.

Recently I had occasion to explore this matter in some more detail and was again struck by the biased and prejudiced attitude that has seeped into the mainstream discourse. In Mathematical Cuneiform Texts (abbreviated in the following as MCT) [1], Otto Neugebauer discusses the YBC 7289, a Babylonian clay tablet dated to about 2000 BCE with the picture of a square and certain numbers in the Babylonian script etched on it in the sexagesimal notation of the Babylonians. A picture of the artifact is shown in the following figure.

YBC 7289

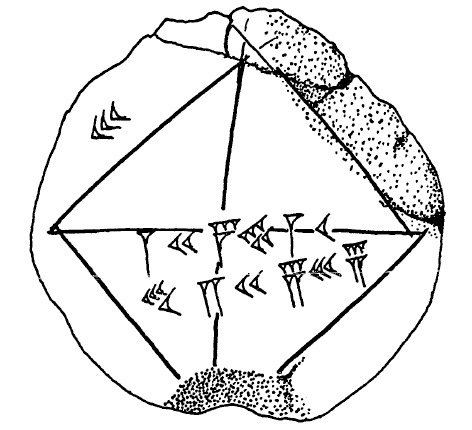
The set on numbers written along the horizontal diagonal of the square are 1, 24, 51, and 10. These are to be interpreted as 1 + 24/60 + 51/60² + 10/60³ in sexagesimal notation, and this is indicated to be the length of the diagonal of a square whose side is 1 unit long. In terms of usual fractions, this equals 30547 / 21600, and in terms of decimal points, equals 1.41421296296...; a remarkably accurate value for √2, differing from it by about 10⁻⁷.

I have discussed Neugebauer’s analysis of YBC 7289 in some detail in an earlier article. There the context is the Sulbasutras and the extremely favorable attitude and assumptions that Neugebauer makes in favor of the Babylonians. As I was going through the section in the MCT where this is discussed, I had a deeper look at some statements which I had not explored in detail earlier and was – once again – surprised at the concessions made in favor of Babylonian mathematics.

To give context to readers who may not have heard about the Sulbasutras, I will give a quick summary about them. The Sulbasutras are a collection of mathematical and geometric rules for creating altars for Vedic rituals. They are part of the Vedas and are dated to about 800 BCE. There are three major Sulbasutras: the Baudhayana, Katyayana and the Apastamba Sulbasutras. The rules concern with, for example, creating an altar whose area is the sum of the areas of two other known altars of the same shape, or creating an altar whose area is equal to the area of another altar but with a different shape, and so on. Among the many rules one finds there are the first ever known statement of the so-called Pythagoras theorem anywhere in the world, a highly accurate value of the square root of two, and various constructions exhibiting sophisticated algebraic and geometric knowledge. For a very good introduction to the Sulbasutras see this article. The main Sulbasutra result we will be discussing in this article is a sutra which gives an approximation to the square root of two. The sutra goes as follows:

and can be translated as

[for finding the square root of two], increase the measure by its third and this third by its own fourth less the thirty-fourth part of that fourth. The name of this increased measure is savisheshah.

and amounts to the following formula:

\(\sqrt 2 \approx 1 + \frac{1}{3} + \frac{1}{3\times 4} - \frac{1}{3\times 4 \times 34}\)

which in fractions equals 577/408. This exceeds the actual value by about 2×10⁻⁶, whereas the Babylonian value is less than the actual value by about 6×10⁻⁷.

Coming back to Neugebauer’s discussion of YBC 7289, at first glance one obviously cannot say if the Babylonians knew that the value they had given was an approximation for the square root of two, or if they believed that it was the exact length of the diagonal of the square. After all, Heath had raised the same objection regarding Apastamba Sulbasutra in 1921:

[…] there is even a construction for √2, or the length of the diagonal of a square with side unity, which is constructed as (1+1/3+1/(3·4)-1/(3·4·34)) of the side: the length taken is of course an approximation to √2 […]; but the author does not say anything which suggests any knowledge on his part that the approximation value is not exact.

Of course Heath was miserably uninformed: the sutra clearly says savisheshah, which means excess, and the Sulbasutra value indeed exceeds the actual value by about 2×10⁻⁶: Thibaut had already stated this in 1875, and Heath’s statement amounts to either sloppy scholarship or to a lack of integrity. Be that as it may, what caught my attention this time was a claim made by Neugebauer on page 43 of MCT that an iterative algorithm for finding the square root of a number was used by the Babylonians to arrive at the stated length of the diagonal. The algorithm goes as follows:

1. Suppose the square root of N is needed.

2. Make an initial guess r₁ for √N.

3. Find r₂ = (1/2)(r₁ + N/r₂), which is the second iteration for √N.

4. Find r₃ = (1/2)(r₂ + N/r₂), which is the third iteration for √N,

Etc., till the desired accuracy is achieved.

The algorithm works because if r_i < √N, then N/r_i > √N. Conversely, if r_i > √N, then N/r_i < √N. Hence √N always lies between r_i and N/r_i, and by successively taking the average of the two, r and N/r approach closer and closer with each iteration, i.e. r approaches √N.

In the following we will call this as the “square root algorithm”.

The relevant part in MCT, where Neugebauer claims this to be the algorithm used by the Babylonians, is shown in the above image. Quoting from the text on page 43 in the above image:

We apply this method [i.e. the square root algorithm] to √2 by starting with (α₁=3/2 as the first rough approximation (α₁² would be 2;15). Then we obtain for the first pair:

α₁ = 1; 30 β₁ = 2/1;30 = 1;20

The next step leads to

α₂ = (1/2)(1;30 + 1;20) = 1;25

β₂ = 2/1;25 = 1; 24; 42; 21

Here we have already reached the above mentioned value √2 approx 1; 25. The very next step leads to

α₃ = (1/2)(1;25 + 1;24;42;21) = 1;24;51;10…

the value given in (1). The fact that both values for √2 found in our texts are links of the same chain seems to be a rather strong argument in support of our explanation.

It is indeed striking that the algorithm gives exactly the same value as the Babylonian approximation at the 3^rd iteration. This seems to be prove quite convincingly that the above algorithm was indeed the one used by the Babylonians to find √2.

After reading the above, I also got taken in, but then I thought, “Wait a minute! this does not mean anything. This is just the sexagesimal representation of a number. Just like 1.41421296296… is its decimal representation. It does not offer any clue as to how it was arrived at. Its value is going to be the same regardless of which method or algorithm you use.” For example, if you take the square root of two using a computer program and find its sexagesimal representation, you will find that the first few numbers will match with the Babylonian value – as indeed they must:

The above code shows the first five “digits” in sexagesimal of the computer generated square root of two, and one can see that the first four (1, 24, 51, and 10) are identical to the Babylonian value. To use the equality of the sexagesimal “digits” of the length of the diagonal with the “digits” obtained from the square root algorithm is therefore like a trick to justify the claim that the square root algorithm was used. Incidentally, this reminds me of a similar trick that was doing the rounds of the internet and social media a few years back. I saw it in the year 2019 and it went like [2]:

It’s amazing: this year is special. It happens only once every 1,000 years. This year your age + your year of birth, every individual is = 2019. For example, you are 55 years old and you were born in 1964, which adds up to 2019. Very strange, even the Chinese and foreign masters can not explain. Please calculate and see if the answer is 2019. It’s a thousand-year wait! Good shot! Go to the circle of friends, let everybody calculate it!

So the sexagesimal representation does not tell us anything. What does give a clue however is the fractional representation. In fractional representation of the Babylonian value is 30547 / 21600. If we start from 3/2 as the initial guess and if we encounter at some point this fraction, then the possibility that the square root algorithm was used becomes a strong one. Let us see if this is the case, starting with, as Neugebauer does, 3/2 as the initial guess:

1) r₁ = 3/2

2) r₂ = (1/2)(3/2 + 4/3) = 17/12

2) r₃ = (1/2)(17/12 + 24/17) = 577/408

3) r₄ = 1/2(577/408 + 816/577) = 665857/470832

Etc.

Nowhere do we encounter the fraction 30547 / 21600 in the above. So on what basis is it claimed that the Babylonians used the square root algorithm for finding the length of the diagonal?

Now we come to the Sulba value of 1 + 1/3 + 1/(3·4) – 1/(3·4·34).

1) The first two terms: 1 + 1/3 = 4/3

2) The first three terms: 1 + 1/3 + 1/(3·4) = 17/12

3) The first four terms: 1 + 1/3 + 1/(3·4) – 1/(3·4·34) = 577 / 408.

We did not encounter the Babylonian 30547 / 21600. But surprise, surprise, at all the three steps the fractions match with the Sulba value. This is obviously a much stronger indication that the square root algorithm was used for deriving the Sulbasutra value instead of the Babylonian value. And if we reduce our standards to those of Neugebauer, that is, compute the sexagesimal representation of the Sulba value and check if they match with the Babylonian value, what do we find? Unsurprisingly, the same sexagesimal “digits” as those of YBC 7289:

The first four “digits” after 1 are identical to the Babylonian “digits”. Thus the Sulba value satisfies not just the standard of “evidence” which was enough for Neugebauer to conclude that the Babylonians used the square root algorithm, but even a much stronger one than that. Why then wasn’t this algorithm proposed by Heath and Neugebauer for the Sulba value? And on what basis does Neugebauer claim that the Sulba value was based on the Babylonian value, as he does in his book Exact Sciences in Antiquity? There is no basis for this claim and neither is this claim backed up by any arguments in his book, except that 17/12 (the first three terms of the Sulba approximation) is mentioned elsewhere on Babylonian tablets [3]. With this standard of evidence the transmission of calculus from India to Europe is a foregone conclusion. Perhaps the only “basis” is the date of 800 BCE assigned to the Sulbasutras which, as we shall see later, is a pretty thin line of evidence to support such grand claims.

In fact, the approximation for √2 given as a sum of fractions in the Sulbasutras offers a much better possibility to reconstruct the method that the Sulbasutra authors could have used. One method is of course the selfsame square root algorithm foisted by Neugebauer on to the Babylonians, as we have seen. But there is also another method that was discussed by Datta and Singh [4] and later extended by Henderson, who even obtained the next few corrective terms in the approximation for √2 [5]. Dropping aside the date of 800 BCE (which is discussed in a later section), this could well have been the method eventually transmitted to the Babylonians.

Obviously this point regarding the fractional representation and the sexagesimal representation must have been noticed by other people also, so I decided to look at the literature in more detail, both at the academic and popular level. I was surprised that most of the articles appeared to assume Neugebauer’s claim as being correct, and from there trying to supply further details on the basis of Babylonian arithmetic and geometry [6]. There was even a teaching project in which material and media are developed to teach school children wherein the supposed use of the square root algorithm in Babylonian mathematics is taught as established fact [7]. Likewise, a pop-article presents the the square root algorithm as if it was part of common knowledge in Babylonia [8].

The one article which most articles were quoting was by Fowler and Robson [9]. I looked into it in detail. It offered a conjectural procedure based on the assumption that the Babylonians knew the approximation √(a²±B) ≈ a ± (½)(B/a), of which there seems to be some evidence. Then 3/2 is used as a first approximation for √2, which is of course in excess. Let (3/2)² – (√2)² = B (here we are following the terminology of Fowler and Robson, where the error term is called B); then B = ¼. So √2 = √((3/2)² – B) = √((3/2)² – 1/4). With a=3/2 and B=1/4 the above approximation can be applied so that √2 ≈ 3/2 – (1/2)(1/4)(2/3), which equals 17/12, which is the approximation to √2 in the first iteration. In the next iteration, the same method is repeated, but with 17/12 as the initial step. This will give 577/408. Do these two numbers sound familiar? Yes, indeed, these are contained in the very same Sulba approximation we saw earlier: 1+1/3+1/(3·4) = 17/12 and 1+1/3+1/(3·4) – 1/(3·4·34) = 577/408. Indeed the method outlined here can be shown to be equivalent to the square-root algorithm, since √N = √(r_i² – B) ≈ r_i – (1/2)(B/r_i). Putting B = r_i² – N in the last expression and after some manipulation we get √N ≈ (1/2)(r_i+N/r_i), i.e. the value at the next iteration for the square root.

Note that in the above discussion, I have given all in terms of the Hindu number system, i.e. the familiar decimal system we use today with zero, place value and the ten symbols 0,1,2,3,4,5,6,7,8, and 9, which makes calculations extremely easy. But remember that the Babylonians were using Babylonian numbers with only two symbols < and Λ and without zero, and where computation is as a consequence several orders of magnitude difficult. In particular, computation was determined critically by the existence of so-called regular and irregular numbers. We run into problems for the second step itself. For the second step, the authors mention that “17/12 is not a regular number”, so they offer two alternatives, (1) that the Babylonians knew some approximation to the reciprocal of 17/12 or (2) that they used the nearest regular number to 17/12. However, what is important is that the authors say

“Both of these alternatives remain conjectural, however, as there is still no direct evidence – by which we mean explicit instructions in the course of a mathematical solution – for the use of more than the first step of the procedure.”

After reading the above one other point became clear to me. There had been the remote possibility that in accordance with Neugebauer the Babylonians had actually used the square root algorithm to get a better approximation, but in the end had truncated the sexagesimal representation to only the first four “digits”, and therefore we do not have the fractional form of 577/408 we see in the Sulbasutras. However the above statements by Fowler and Robson show that things were not as straightforward, especially with regard to the number system used by the Babylonians. The arithmetic hurdles they would have had to overcome were high indeed. It is only the ease of calculation which the Hindu number system provides us and to which we are so accustomed which makes us prone to overlook such details.

This article by Fowler and Robson is one of the most quoted ones to support the use of the square root algorithm by the Babylonians, but as shown, a closer perusal of the article reveals that the authors themselves make no such sweeping claims and are candid that it is a reconstruction and “conjectural”. Similarly, the article “Pythagoras Theorem in Babylonian Mathematics” on the Mactutor archive of mathematics [10] says that

… there is no evidence of the algorithm being used in any other cases and its use here must remain no more than a fairly remote possibility.

In spite of this, most papers and pop-articles present it as obvious fact.

Another point is that none of the articles seem to look at the concerns I have raised, viz. fractions vs. the sexagesimal value of Babylonians, in more detail. This even made me doubt if I was even on the right track. Was I missing something here? It could well be. But on the other hand, could it be that everyone is just taking the claims of Neugebauer uncritically, since they come from an “authority”? And haven’t we seen enough examples of bias against the Sulbasutras, even though the Sulba value is a much more possible candidate for being derived from the square root algorithm? And on a side note, is this how conjecture becomes fact? Why are certain conjectures amplified and certain others discarded? Why not, for example, amplify the analyses and results of Leopold von Schroeder, or David Henderson, or Abraham Seidenberg, or Conrad Müller, whose works imply that the Sulbasutras or “something very similar to the Sulbasutras” were the origins of Babylonian geometry (Seidenberg), or the presence of an implicit proof of the “Pythagoras Theorem” in the Sulbasutras (Müller), or the interaction of Pythagoras with the Brahmins of India, from whom he could have got both his philosophical and mathematical ideas (von Schroeder) (assuming Pythagoras knew it in the first place), or the presence of a geometric method closely related to the square root algorithm (Henderson) [11-14]?

The Date of 800 BCE for the Sulbasutras

Whereas the Babylonian clay tablets are dated to around 2000 to 1600 BCE, the date usually assigned to the Sulbasutras is around 800 BCE, i.e. about 1200 years posterior to the Babylonian mathematics. This is the one and only basis for claims that the Sulbasutras are derived form Babylonian geometry or, even if the independence of the Sulbasutras is granted, for the assumption that they could not have had any influence on the development of Babylonian geometry. The consequence has been that the Sulbasutras have been practically pushed out of the picture by Babylonian geometry in mainstream accounts. As Seidenberg said [15, 16]:

Perhaps with the date of 1700B.C. for Old-Babylonia well in hand, the question of whether Vedic geometrical knowledge dates from 200 A.D., or 100 B.C., or 300 B.C., or 500 B.C., or even a 1000 B.C., faded into insignificance.

And

Anyway, the damage had been done and the Sulvasütras have never taken the position in the history of mathematics that they deserve.

There are enough indications that exactly this was the intention, as we have seen in earlier articles.

But as we have seen, it is easy for conjectures to become “facts”, so this date of 800 BCE must also be examined in more detail. To begin with, there has always been a near unanimity among traditional Sanskrit scholars in India that the Vedas, including the Sulbasutras, are much older than 800 BCE. Next, the date of 800 BCE assigned by Indologists was done in an era when postdating the Vedas was the norm, and so any date given by them must be taken as an upper bound, and a liberal one at that. Thirdly, we turn to two articles by Seidenberg, where he analyses the Sulbasutras, Greek geometry and Babylonian geometry in great detail and comes to the conclusion that both Greek geometry and Babylonian geometry have their origin in a mathematics which is very similar to the Sulbasutras [17].

A comparison of Pythagorean and Vedic mathematics together with some chronological consideration showed that the current view [of Greek influence on Vedic thought] is not tenable. A common source for the Pythagorean and Vedic mathematics is to be sought either in the Vedic mathematics [i.e. the Sulbasutras] or in an older mathematics very much like it. The view that Vedic mathematics is a derivative of Old-Babylonian having been rejected, a common source for these mathematics, different from Old-Babylonia of 1700 B.C., was indicated. Thus what are regarded as the two main sources of Western mathematics, namely Pythagorean mathematics and Old-Babylonian mathematics, both flow from a still older source.

What was this common, older source like? I think its mathematics was very much like what we see in the Sulbasutras.

Seidenberg’s hypothesis of a “common older source” depends critically on the assumption of an “Aryan invasion” which, as we know today, was a fabrication of race-obsessed European scholars of the 19^th and 20^th centuries. No evidence for an ‘older, common source’ has been found either, and if the supposed ‘older, common source’ is ‘very much like what we see in the Sulbasutras’, there is no reason why it should not be the Sulbasutras themselves. And as Thibaut says, anything that has to do with religion in the Hindu civilization must be considered indigenous to India [18]. All these bits of the puzzle fall neatly into place by assuming that the Sulbasutras are much older than the assumed dates and are the common source of Babylonian and Greek geometry which Seidenberg is referring to in the above.

Summary

In summary, we can note the following points:

1. Neugebauer clearly implied the Babylonians used the square root algorithm to find the square root of two.

2. However from the value itself, given in sexagesimal notation of the Babylonians, itself offers no clue how it was arrived at. (For example, you can find π by the polygon method, or by summing up an infinite series, but the end result expressed in decimals will give you no clue how you arrived at the value. I’m of course assuming that only the correct digits after the decimal/sexagesimal are retained, like in the Babylonian value for square root of 2.)

3. The fractional representation, which is a better indication, does not occur in the iterations of the square root algorithm, thus not supporting the hypothesis that this algorithm, foisted on to the Babylonians in hindsight, was indeed used.

4. The Sulbasutra result is given in fractions, in fact it is given as a sum of fractions and each successive term increases the accuracy of the approximation. Successively including these terms yield fractions that exactly correspond with the approximations that occur in the successive iterations of the square root algorithm (17/12 and 577/408).

5. A careful look at the references do not offer any evidence that the square root algorithm was indeed used. The use of this algorithm has been termed as “conjectural”.

6. Yet several sources in the literature claim the use of this algorithm as “established fact”.

7. This has to be compared with the statements of Heath and Neugebauer regarding the Sulba value for the approximation of √2. Compare also with Cantor: he claimed on the basis of the dates assigned to the Sulbasutras that they were derived from Greek geometry. Later when this view became untenable he claimed that Greek geometry was derived from Egypt but not India, even though the Sulbasutras may be anterior to Greek geometry and uninfluenced by the latter – anything to keep India out of the picture. Now it comes back full circle with a later scholar (Neugebauer) again imputing a foreign influence on the Sulbautras, and again on the basis of the dates assigned to them.

8. The justification for the erasure of the Sulbasutras from history hinges critically on the date of 800 BCE assigned to them. As we have seen, there are strong indications that they are much older and that the source of the mathematics from the Babylonian region is to be found in the Sulbasutras.

Final Note

Since the domination of Babylonian mathematics and the obliteration of the Sulbasutras from mainstream history of mathematics hinges critically on the dates assigned to the Sulbasutras, and since the assumption of a date for the Sulbasutras either contemporary or prior to the Old-Babylonian civilization would take care of several inconsistencies which the currently assumed dates give rise to, such as Seidenberg’s observation that Babylonian mathematics was based on an older mathematics “very much like what we see in the Sulbasutras”, and would moreover obviate the need for inventing this older mathematics which depends on the flawed assumption of a supposed Aryan invasion, it is vitally important for Hindu scholars to carefully examine (1) the exact nature and (2) the basis of the claims of 800 BCE as the date of the Sulbasutras made by European Indologists during the colonial era, and to come up with dates that more reliably reflect the time in which the Sulbasutras were composed.

References

[1] Neugebauer, Otto. Mathematical Cuneiform Texts, American Oriental Series, Volume 29, 1945.

[2] https://www.aap.com.au/factcheck/age-and-birth-year-claim-doesnt-occur-every-1000-years/ and

https://sustainingcommunity.wordpress.com/2017/10/22/math-not-phenomenon accessed April 13 2014.

[3] Otto Neugebauer. The Exact Sciences in Antiquity, 2^nd edition, Dover Publications, New York, p. 35.

[4] Datta, Bibhutibhushan. The Science of the Sulba: A Study in Early Hindu Geometry. University of Calcutta, 1932.

[5] David W. Henderson, Square Roots in the Sulbasutras, Geometry at Work: Mathematical Association of America Notes Number 53, 2000.

[6] For example Mansfield Daniel F., Mesopotamian square root approximation by a sequence of rectangles, British Journal for the History of Mathematics Volume 38, 2023 - Issue 3.

[7] https://static1.squarespace.com/static/548c7255e4b0dc7d9090548f/t/5931913debbd1aba50c75d1f/1496420670391/Babylonian+algorithm.pdf, accessed April 13, 2024.

[8] https://thepalindrome.org/p/how-did-the-babylonians-know-2-up, accessed April 13, 2024.

[9] David Fowler and Eleanor Robson, Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context, Historia Mathematica 25 (1998) 366-378. Available online at https://www.sciencedirect.com/science/article/pii/S0315086098922091.

[10] https://mathshistory.st-andrews.ac.uk/HistTopics/Babylonian_Pythagoras/, accessed April 13 2024.

[11] Leopold von Schroeder, Pythagoras und die Inder: eine Untersuchung über Herkunft und Abstammung der Pythagoreischen Lehren. Leipzig: 1884.

[12] David W. Henderson, Square Roots in the Sulbasutras, Geometry at Work: Mathematical Association of America Notes Number 53, 2000.

[13] A. Seidenberg. The Origin of Mathematics. Archive for History of Exact Sciences, Vol. 18, No. 4, (1978): pp. 301-342.

[14] Conrad Müller. Die Mathematik der Śulvasûtra. Eine Studie zur Geschichte indischer Mathematik, Abh. Math. Semin. Univ. Hambg. 7, 173–204 (1929).

[15] A. Seidenberg. ‘The Ritual Origin of Geometry.’ Archive for History of Exact Sciences, Vol. 1, No. 5, (1962): pp. 488-527.

[16] A. Seidenberg. The Origin of Mathematics. Archive for History of Exact Sciences, Vol. 18, No. 4, (1978): pp. 301-342.

[17] A. Seidenberg. The Origin of Mathematics. Archive for History of Exact Sciences, Vol. 18, No. 4, (1978): pp. 301-342.

[18] G. Thibaut. On the Śulvasûtras. Journal of the Asiatic Society of Bengal, 1875, p. 227.